Review on Testers for Measuring Flow Properties of Bulk Solids

Abstract

Currently, pressure from industry to streamline processes by creating their simulation models, and thus to gradual digitization is increasing. The essence of representative simulation models of bulk materials is to understand the principles and laws of the real beliefs of particles. The aim of this report is therefore to detect and quantify the possibilities and principles of how particles tin modify their position relative to other particles. The possibilities of particle displacements were expressed using their specific trajectories and work ratios, or internal friction angle values. This created a new comprehensive model of the internal friction angle of particles independent of particle size. It enables the estimation of the determined values of the angles of internal friction of particles and its application in the field of simulations of mass and process models. The model tin be used to determine the basic limerick of particles in volume and the dominant means of their mutual displacements.

Introduction

In the field of particulate material mechanics, it may seem that the general question of particle displacement is solved by the assumption of quasi-linear motility based on infinitesimal or at least sufficiently small particles compared to the space in which they motility. The example might be shear stress versus ratio of shear cell bore D to particle size¹.

Shear tests to determine the parameters of friction and flow are very suitable methods for describing the properties of particulate materials^ii,three,4,5. Shear auto manufacturers use unlike shear jail cell designs and, based on size, also recommend unlike ratios of maximum particle size to the feature size of these cells^6,7.

In Jenike's direct shear exam, the shear plane is not ideally horizontal^1,6. The bodily shear management deviates angularly from the imaginary horizontal shear plane. Information technology is more than of a shear zone than a plane. Particle size and normal loading have a significant effect on the properties of the shear zone. Numerous experiments were performed on Jenike'southward shear examination, where the shape of the shear zone was demonstrated, for example, by X-ray scanning^eight.

The current state of particle research allows for more detailed studies of particle beliefs using discrete element simulations (DEM). Lots of works accept focused on efficiently determining the optimal particle shape for simulation processes^ix,10. These process methods are validated according to the volumetric behaviors of the materials. There is a direct correlation with the upshot of particle shape backdrop on volumetric and strength behavior together with the change in internal friction bending¹¹. To evaluate the circuitous material properties based on internal friction, the effect of particle shape on internal friction can exist included.

Shear tests have been the subject of much research focusing on DEM¹². The variety of force distribution, particle directions and velocities, and the effect of particle size on the shear zone, its shape and size were also demonstrated using DEM simulations^{thirteen,fourteen}. The results of experiments and simulations show that the shear zone is non a horizontal plane and its shape is demonstrably related to particle displacements.

An ideal shear plane would be created by precise shear (cantankerous-section) of particles in a shear cell, or by the shear of infinitesimal particles.

Dilatancy in granular materials is some other of import concept¹⁵. Dilatation here means a change in volume which is acquired past quasi-static shear deformation. Reynolds stated that the angle of friction used by Rankin is a macroscopic quantity "Related to the system of particles"^xvi. It has been proven that friction between particles is much less important in determining the strength of granular materials in macro-dimensions than their "arrangement"^16,17,18.

The very essence of the continuum of dry crystalline materials practical to the principles of shear cell and particle size ratios can be further understood every bit the number of possibilities of irresolute the position of particles in a volume element (space) relative to each other.

If it were shown that one particle has a express number of possibilities to change its position relative to other particles, then the total number of changes in the position of all particles will besides be quantifiable (final).

This paper describes a new perspective on the internal friction angle of particles. The proposed model is based on a non-zero particle size with a symmetric shape that is embeddable in a sphere (basic shapes).

Historically, there are some tendencies to simplify the estimation of internal friction through an angle of repose, e.one thousand.^nineteen. This study focuses on the partial furnishings of particle shifts, which tin occur as macro properties of matter (angle of repose, etc.).

Internal friction angle model of particles

Mechanical work is given by the scalar product of force and path. In particle mechanics, it is the production of the external strength interim on the particle and the magnitude of its deportation. In full general, much attention has always been paid to questions of force interactions betwixt particles, while minimal attention has been paid to the question of determining the possible trajectories of particles as their position relative to the environment changes. The fact is that for the determination of mechanical work, both strength and displacement touch on the resulting value in the scalar product of force and trajectory.

The infinitesimal increment of mechanical work is given by the scalar product d W (i), where F is the force acting on the particle and d due south is an infinitesimal displacement vector along the trajectory of the particle. Equation (2) then applies to three-dimensional vectors.

$$d{\varvec{W}} = {\varvec{F}}\cdot d{\varvec{s}}$$

(1)

$$dW = F_{x} \cdot dx + F_{y} \cdot dy + F_{z} \cdot dz$$

(two)

Full general definition of the internal friction angle

The general definition of internal friction is based on energy rest which describes the power of particles of thing to practise piece of work.

The situation in Fig. 1 assumes dry (Coulomb) friction without actual rotation of bodies where the kinetic friction force T is equal to the product of the kinetic friction coefficient tan(φ) and the normal strength N and its direction is opposite to the skid management. The path of bodies (particles) is given by their shape.

Figure 1

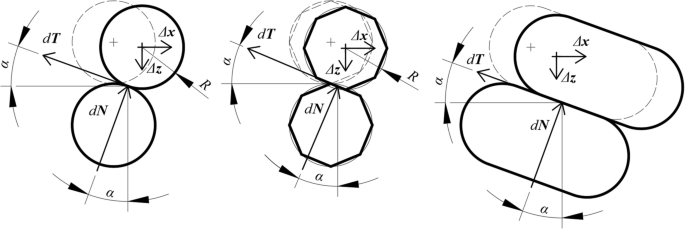
Diagram of the work of particles during displacement.

Full size prototype

The ratio of the works dW1 and dW2 tin can be considered every bit a generalized tangent of the angle of internal friction and this ratio can be written in the following grade (run across Eq. 3):

$$\tan (\varphi ) = \frac{{dW_{1} }}{{dW_{ii} }} = \frac{{\left\| {d{\varvec{T}}} \right\| \cdot \left\| {\Delta {\varvec{ten}}} \right\| \cdot \cos (\alpha )}}{{\left\| {d{\varvec{N}}} \correct\| \cdot \left\| {\Delta {\varvec{z}}} \right\| \cdot \cos (\alpha )}} = \frac{{d{\varvec{T}} \cdot \Delta {\varvec{ten}}}}{{d{\varvec{Due north}} \cdot \Delta {\varvec{z}}}}$$

(3)

where α is the angle between the vectors d T and Δ x or the vectors d North and Δ z . The basic model assumes that the strength vectors are parallel to the displacement vectors if the bending α is zero or approaches the limit of aught (Eq. 4).

$$\mathop {\lim }\limits_{\alpha \to 0} (\cos (\alpha )) = \cos (0) = 1$$

(4)

Then, the ratio of force magnitudes volition be equal to parameter B

$$B = \frac{{\left\| {d{\varvec{T}}} \right\|}}{{\left\| {d{\varvec{N}}} \correct\|}}$$

(5)

and the ratio of the size of the displacement volition be equal to parameter C.

$$C = \frac{{\left\| {\Delta {\varvec{x}}} \right\|}}{{\left\| {\Delta {\varvec{z}}} \correct\|}}$$

(6)

Solving the ratio defined in Eq. (3) leads to three possible interpretations of friction which are given by the atmospheric condition:

• Pocket-sized or symmetrical displacements and greater friction forces (Eq. 5)

• Larger displacements and smaller magnitude friction forces (Eq. 6)

• Combination of both (Eqs. five and 6)

Small or symmetrical displacements and greater magnitude friction forces

If nosotros do not know the ratio of the deportation lengths of the particles C, we can solve the state of affairs past bold very small (infinitesimal) particles (with a characteristic radius R → 0). When their displacements ǀǀΔxǀǀ and ǀǀΔzǀǀ are infinitesimally small, the job tin exist defined by the limit of the ratio of the respective displacements (Eq. 7). The influence of small particle size is the field of study of papers dealing with the determination of purlieus conditions for measurability of samples on shear machines^ane,20,21.

$$\mathop {\lim }\limits_{{\left\| {\Delta x} \correct\| \to 0 \wedge \left\| {\Delta z} \right\| \to 0}} (C) = one$$

(7)

The characteristic radius R represents the maximum grain size. Ideally, the shape is symmetrical and spherical, but in the real world it is fabricated upwards of infinitely many surfaces. For simpler graphical representation in this paper, the real shape of the particles formed by asymmetrical surfaces will exist replaced by a spherical shape.

The parameter that depends on the characteristic particle size (on the characteristic radius R) is parameter C (Eq. half-dozen). It expresses the influence of the geometric parameters of the particles on the value of the internal friction angle.

For the limiting example of particle size budgeted zero, we can write the existential status of parameter C (displacements ǀǀΔ 10 ǀǀ and ǀǀΔ z ǀǀ are a function of particle size with characteristic radius R), or have particles such that R → 0 ⇒ ǀǀΔ x ǀǀ → 0 ∧ ǀǀΔ z ǀǀ → 0. If we are dealing with lengths of deportation vectors ǀǀΔ ten ǀǀ and ǀǀΔ z ǀǀ approaching nada, we can afford to assume that their ratio is equal to 1.

It follows from this that for a particle size of zero, the dissipative piece of work ratio in Eq. (3) is not a role of the displacement vectors, but a ratio of the magnitudes of the forces. The tangent of the internal friction angle (Eq. eight) is given by the production of the ratio of the magnitudes of the forces B (Eq. 5) and the ratio of the magnitude of the displacement C = 1 (Eq. 6).

$$\tan (\varphi ) = \frac{{\left\| {d{\varvec{T}}} \right\|}}{{\left\| {d{\varvec{N}}} \correct\|}}$$

(8)

Under ideal atmospheric condition and for not-zero symmetrical particle sizes (without deformations, particle degradation and moisture), particle displacements occur in the shear cell while maintaining the sample volume. If the volume is constant, information technology is possible that there is a finite number of possible particle displacements limited by duration (fourth dimension). In the instance of a rotary shear test, there is no path constraint dictated by geometry and the bones displacements may repeat in cycles (Fig. 2).

Figure 2

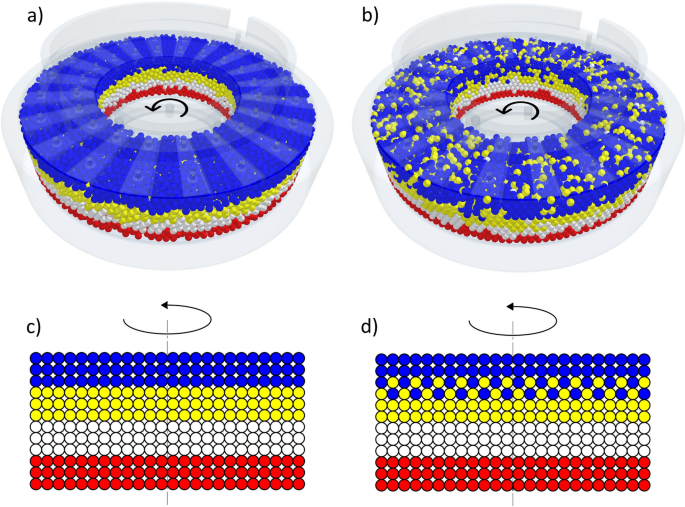
Particle displacement. (a) Initial position of the rotary examination, (b) last position of the rotary examination, (c) schematic representation of the initial position, (d) schematic representation of the displacement.

Full size image

Equation (8) tin can also assume that ǀǀΔ x ǀǀ = ǀǀΔ z ǀǀ fifty-fifty if the ratio of lengths C would be 1. This situation is explained in Fig. three. The upper particle is in contact with the lower and shifts by ǀǀΔ x ǀǀ = ǀǀΔ z ǀǀ, or both particles can shift by the same values of ǀǀΔ x ǀǀ and ǀǀΔ z ǀǀ.

Figure 3

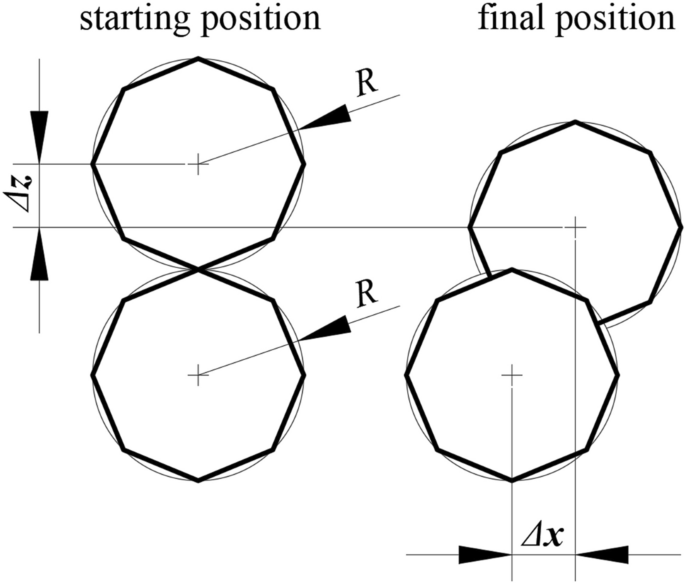
Possibility of symmetrical values of displacements ǀǀΔ x ǀǀ and ǀǀΔ z ǀǀ.

Total size paradigm

Assuming a particle size of zippo or ǀǀΔ x ǀǀ = ǀǀΔ z ǀǀ, we tin also write Eq. (9) for the shear stress and Eq. (10) for the normal stress. It tin also be assumed that the shear surface Aτ is equal to the normal surface Aσ, i.e., Aτ =Aσ =A, and therefore the tangent of the inner angle of friction is usually written as Eq. (eleven).

$$\tau = \frac{dT}{{dA}} = \frac{{\left\| {d{\varvec{T}}} \right\|}}{{A_{\tau } }}$$

(9)

$$\sigma = \frac{dN}{{dA}} = \frac{{\left\| {d{\varvec{North}}} \right\|}}{{A_{\sigma } }}$$

(10)

$$tan(\varphi ) = \frac{\tau }{\sigma }$$

(11)

Small-scale magnitude friction forces, large displacements

Assuming that the magnitude of the forces performing the work approaches zippo, we can solve Eq. (three) analogously based on the limit of the ratio of the magnitude of the forces B (see Eq. 5) with the condition of the magnitude of the forces approaching zero. Particles of matter are only displaced by external forces in the surround (affecting other particles). Particles of matter move, for example, by passing through the gaps betwixt particles. Particles fall through and friction fluctuates (transitions betwixt static and kinetic friction, or skid-stick consequence) due to the unevenness of the surfaces formed by the particles when the particles movement amid each other.

If we are dealing with the magnitudes of vector forces ǀǀd T ǀǀ and ǀǀd North ǀǀ approaching nothing, or if the internal friction bending φ → 0 ⇒ ǀǀd T ǀǀ ≈ ǀǀd N ǀǀ (perfect fluid/inviscid fluid), we can afford to introduce a similar assumption as used in section "Minor or symmetrical displacements and greater magnitude friction forces", namely that the ratio of the magnitude of the forces B is equal to 1, or

$$\mathop {\lim }\limits_{{\left\| {d{\varvec{T}}} \correct\| \to 0 \wedge \left\| {d{\varvec{N}}} \right\| \to 0}} (B) = 1$$

(12)

It follows that the tangent of the bending of internal friction is given by the product of the ratio of the path lengths C and the ratio of the magnitude of the forces equal to 1, or

$$tan(\varphi ) = \frac{{\left\| {\Delta {\varvec{x}}} \right\|}}{{\left\| {\Delta {\varvec{z}}} \right\|}}$$

(thirteen)

Equation (13) represents a situation where the magnitude of the strength ratio B is negligible with respect to the magnitude of the path ratio C. The internal friction angle of the particles is then defined independently of the force effect and is dependent on the displacement of the particles for particle systems.

Combination of modest or symmetrical displacements with greater frictional force and modest frictional forces with large displacements

Proportional dissipative work tin be expressed past the tangent of an bending φ:

$$tan(\varphi ) = B \cdot C$$

(14)

where both parameters are nonzero. The solution is complicated because both the ratio of force magnitudes and the ratio of displacement lengths are circuitous functions of many physical quantities and the solution is subject field to the definition of complicated contact tasks, the solvability of which is still determined by the caste of optimization of mathematical models in calculating specific solutions.

Overview of particle deportation possibilities

The model of internal friction of particles is based on the basic shape contacts of particles and the differences in altitude between the particles of these shape contacts. The first group T₁₁–T₁₅ (Fig. 4) is characterized by the fact that the active particle "goes effectually" the passive particle²². The second group T₂₁–T₂₅ (Fig. iv) is characterized in that the active particles displace passive particles. Figure 4 shows the initial and terminal position of the particle of the individual particle movements.

Effigy iv

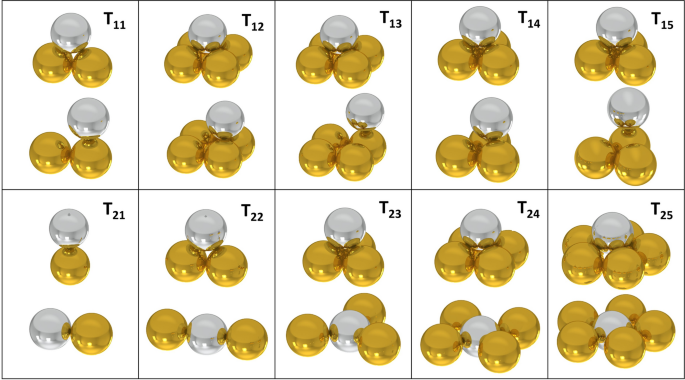
Initial and terminal positions of the displacements T₁₁–T₁₅ and T₂₁–T₂₅.

Total size image

The value of Δz represents the maximum possible path of the particle in the vertical management and besides the top deviation of the position of the particle. The calculation was performed equally the difference between the maximum and minimum height values for the displacements T₁₁–T₁₅ that the spherical contour of the particle tin can perform (Eq. 15). For T₂₁–T₂₅ shifts, the value of Δz is directly equal to the maximum superlative (Eq. 16). The value of Δx represents the displacement of the particle in the horizontal management so that the maximum value of Δz is ever attained. Each displacement is specific in its ain combination of Δz/Δx values and is independent of the particle radius R parameter (Table one). Tabular array 2 and so shows the work ratios dW1 and dW2, or value tan(φ) and internal friction bending of particles φ.

$$\Delta z = H_{max} - H_{min}$$

(xv)

$$\Delta z = H_{max}$$

(16)

Table ane Parameters Δz and Δx of individual displacements T₁₁–T₁₅ and T₂₁–T₂₅.

Full size table

Table 2 Summing up of tan(φ) and φ of private displacements T₁₁–T₁₅ a T₂₁–T₂₅.

Full size table

Mean probable angle of internal friction of particles

With the aforementioned probability of attainment of the number n of individual displacements, the mean probable angle of internal friction of particles φc can be expressed by Eq. (17). The coefficient k _Tij represents the probability of private displacement T₁₁–T_fifteen and T₂₁–T₂₅. In our model instance, k _T11–k _T25 equals the value 1 and afterward achieving φc = 39.ii°.

$$\varphi_{c} = \frac{{\sum k_{{T_{ij} }} \cdot \varphi_{{T_{ij} }} }}{n}$$

(17)

Experimental measurement of the internal friction angle of crystalline material

Due to its stable crystallization in a cubic arrangement and the possibility of inserting a crystal shape into a sphere, a dry crystalline fabric in the form of NaCl table salt was called (Fig. 5). Particle size distribution was measured on devices Camsizer Retch and Cillas 1190. The Table 3 shows the measured particle size values. The designation of the salt samples is the aforementioned as in Fig. 5.

Figure v

View of the grains of the measured salt samples, (a) edible iodized common salt, (b) pure natural salt, (c) fine sea table salt, (d) fibroid-grained sea salt, (e) Sicilian fine salt, (f) dehydrated bounding main common salt, (grand) fine coastal ocean salt, (h) Sicilian coarse-grained salt, (i) edible stone salt, (j) Italian coarse-grained sea salt.

Full size epitome

Table iii Particle size distribution of salt samples.

Full size table

The measurement of internal friction was performed on a Ring Shear Tester RST-01.pc. The normal load for Pre-Shear was gear up at 20, ten, 5 kPa. Individual normal loads were measured ten times. The everyman measured value of the normal load for shear was set to 10% of the normal load for Pre-Shear and the number of stress levels was 6.

The angle of internal friction at steady-state flow φsf was averaged both for the partial normal load for Pre-Shear (twenty, 10, 5 kPa) and for all three of these stresses of each salt sample. The resulting value of φsfC was then arrived at past averaging all values of φsf. This angle characterizes the internal friction at steady land flow in the section aeroplane (friction majority solid / bulk solid)^iii,seven. Tabular array 4 summarizes the measured φsf values.

Table four Average values of φsf for 20, x, v kPa and overall boilerplate values of salt samples a-j.

Full size tabular array

Figure 6 shows an overview of experimental φsf data processed into a Gaussian distribution for individual salt samples, but also as a whole every bit for one set of φsfC salt samples. Furthermore, the derived mean probable angle of internal friction of particles φC is indicated here. Since at that place is no perfect overlap of these two values, information technology can be concluded that the probability of individual displacements under consideration is not uniform or the same as considered in the model, just tends to a certain imbalance.

Figure 6

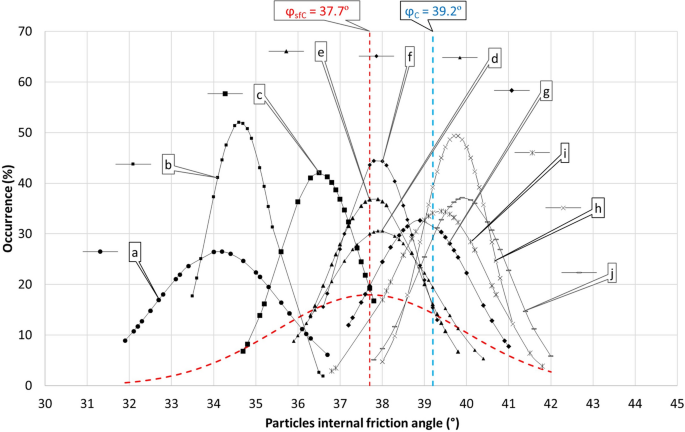
Gaussian distribution φsf for private samples, for the whole set of samples φsfC and mean probable angle of internal friction of particles φC.

Total size paradigm

Conclusion

The paper introduces the principle of describing the internal friction of particles using a probabilistic model of particle shape displacements. A relationship was found between the model of shape angles of internal friction of particles and experimentally determined bending of internal friction of particles at steady menses. The germination of particle displacement and the balance of internal friction are based on changes in the positions of the particles relative to the environmental changes in their positions.

The nature of the motion of both individual particles and their sets within the body of particulate thing implies that the accomplishment of motion is conditional upon the motion autonomy of individual particles and their clusters. The autonomy of movement of individual particles makes it possible to characterize the period capabilities of non-cohesive bulk materials.

The model presented in this paper is based on the description of the backdrop of the motion of matter:

• particles can change their position based on shape contacts which define the weather condition of their movement

• the way in which particles modify their position is the dominant factor characterizing matter in terms of dissipation work needed to accomplish these movements

• the way in which the particles alter their position determines the free energy intensity of the mass system and thus the size of the angle of internal friction of the particles

• with the same probability of all particle displacements, the mean likely angle of internal friction of the particles is 39.two°.

The presented model enables both the interpretation of the measured values of the internal friction bending and the application of the measured values in the field of simulations of mass models and mechanical processes.

The trajectory of moving particles of particulate matter may not always be direct dependent on external forces exerting mechanical piece of work. Internal friction can be understood as a measure of loss work and the angle of internal friction equally a ratio of loss work. The work performed, i.e., the scalar product of the external force and the particle trajectory, is the production of 2 independent quantities. The external force is a office of the external inputs and the trajectories are a function of the position of the particles (particle configuration) before motion and changes in their positions during motion.

Active particles mostly have ii means in which they tin can change their position relative to the surrounding particles. The first manner is that the agile particles do not push the passive particles out of their positions, but move effectually them. The second method is that the active particles push the passive particles out of their positions and occupy the original position of the passive particles.

References

1. Schwedes, J. Review on testers for measuring flow properties of bulk solids. Granul. Affair 5, 1–43 (2003).

   ADS  Commodity  Google Scholar

2. McGlinchey, D. Characterisation of Bulk Solids (Blackwell, 2005).

   Book  Google Scholar

3. Schulze, D. Powders and Bulk Solids (Springer, 2008).

   Google Scholar

4. Rhodes, 1000. J. Introduction to Particle Engineering (Wiley, 2008).

   Book  Google Scholar

5. Feda, J. Mechanics of Particulate Materials (Elsevier, 1982).

   Google Scholar

6. Jenike, A. W. Storage and Flow of Solids (University of Utah, 1964).

   Google Scholar

7. Schulze, D. Ring Shear Tester RST-01.pc Operating Instructions v2.0 (Dietmar Schulze, Wolfenbüttel, 1999–2011)

8. Janssen, R. J. M. Structure and Shear in a Cohesive Pulverisation (Delft University of Technology, 2001).

   Google Scholar

9. Suhr, B. & Six, Grand. Simple particle shapes for DEM simulations of railway ballast: Influence of shape descriptors on packing behaviour. Granul. Matter 22, 1–17 (2020).

   Article  Google Scholar

10. Pourtavakoli, H., Parteli, East. J. & Pöschel, T. Granular dampers: Does particle shape thing?. New J. Phys. eighteen, 073049 (2016).

    ADS  Article  Google Scholar

11. Kozicki, J., Tejchman, J. & Mróz, Z. Event of grain roughness on strength, volume changes, elastic and dissipated energies during quasi-static homogeneous triaxial pinch using DEM. Granul. Matter 14, 457–468 (2012).

    Commodity  Google Scholar

12. Tykhoniuk, R., Jürgen, T. & Luding, South. Shear dynamics simulations of loftier-disperse cohesive powder. In Particulate Systems Assay, one–v (2003).

13. Salazar, A., Sáez, E. & Pardo, 1000. Modeling the direct shear test of a fibroid sand using the 3D Discrete Element Method with a rolling friction model. Comput. Geotech. 67, 83–93 (2015).

    Article  Google Scholar

14. Kozicki, J., Niedostatkiewicz, Thou., Tejchman, J. & Muhlhaus, H. B. Discrete modelling results of a direct shear test for granular materials versus FE results. Granul. Matter 15, 607–627 (2013).

    Article  Google Scholar

15. Reynolds, O. LVII. On the dilatancy of media equanimous of rigid particles in contact. With experimental illustrations. Philos. Magazine. J. Sci. 20, 469–481 (1885).

    Commodity  Google Scholar

16. Kruyt, Due north. P. & Rothenburg, L. A micromechanical study of dilatancy of granular materials. J. Mech. Phys. Solids 95, 411–427 (2016).

    ADS  MathSciNet  CAS  Commodity  Google Scholar

17. Skinner, A. E. A note on the influence of interparticle friction on the shearing strength of a random associates of spherical particles. Geotechnique xix, 150–157 (1969).

    Commodity  Google Scholar

18. Rowe, P. W. The stress-dilatancy relation for static equilibrium of an assembly of particles in contact. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 269, 500–527 (1962).

    ADS  Google Scholar

19. Metcalf, J. R. Angle of repose and internal friction. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 3, 155–161 (1966).

    Commodity  Google Scholar

20. Shi, H., Luding, S. & Magnanimo, 5. Limestone powders yielding and steady land resistance under shearing with dissimilar testers. In 2d International Conference on Powder, Granule and Majority 1–6 (2016).

21. Shinohara, K. & Golman, B. Dynamic shear properties of particle mixture by rotational shear examination. Pulverisation Technol. 122, 255–258 (2002).

    CAS  Article  Google Scholar

22. Zegzulka, J. The angle of internal friction equally a measure of work loss in granular fabric menstruation. Powder Technol. 233, 347–353 (2013).

    CAS  Article  Google Scholar

Download references

Acknowledgements

This paper was conducted within the framework of the project Innovative and condiment manufacturing technology—new technological solutions for 3D press of metals and blended materials, reg. no. CZ.02.i.01/0.0/0.0/17_049/0008407 financed by Structural Founds of Europe Wedlock and of the grant of SGS No. SP2021/55, Faculty of Mining and Geology, VSB—Technical University Ostrava, Czech Republic.

Writer information

Affiliations

1. VSB-TU Ostrava, CEET, ENET Eye, Bulk Solids Middle, 17. listopadu 15, 708 00, Ostrava, Czechia

   Jiri Zegzulka, Jan Necas, Jiri Rozbroj & Lucie Jezerska

2. Department of Mining Engineering and Safety, Kinesthesia of Mining and Geology, VSB-TU Ostrava, 17. listopadu fifteen, 708 00, Ostrava, Czechia

   Jiri Zegzulka, January Necas, Jiri Rozbroj & Daniel Gelnar

3. Department of Mechanical, Chemical and Industrial Design Engineering science, Universidad Politécnica de Madrid, Ronda de Valencia 3, 28012, Madrid, Spain

   Álvaro Ramírez-Gómez

Contributions

All authors have read and agreed to the published version of the manuscript. J.Z. discovered the mechanisms. J.R. wrote the main manuscript text. L.J. and J.N. corrected the text. J.Z., D.G. and Fifty.J. designed the experiments. D.G., J.R. performed the experiments. D.G., J.R. and A.R-G. analysed the data.

Corresponding author

Correspondence to Lucie Jezerska.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher's note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Artistic Eatables Attribution four.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long equally you lot give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party textile in this article are included in the article's Artistic Commons licence, unless indicated otherwise in a credit line to the material. If cloth is not included in the article'southward Artistic Commons licence and your intended use is not permitted past statutory regulation or exceeds the permitted use, y'all will need to obtain permission straight from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/iv.0/.

Reprints and Permissions

Nearly this article

Cite this commodity

Zegzulka, J., Necas, J., Rozbroj, J. et al. Internal friction angle model of particles. Sci Rep 12, 2036 (2022). https://doi.org/10.1038/s41598-022-05891-eight

Download citation

• Received: 13 September 2021

• Accepted: 13 January 2022

• Published: 07 February 2022

• DOI : https://doi.org/10.1038/s41598-022-05891-8

Comments

By submitting a annotate you lot concur to abide by our Terms and Community Guidelines. If you observe something abusive or that does not comply with our terms or guidelines please flag it every bit inappropriate.

navarretetere1988.blogspot.com

Source: https://www.nature.com/articles/s41598-022-05891-8

Share this post